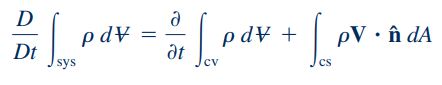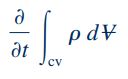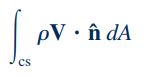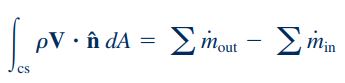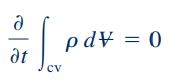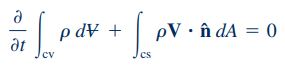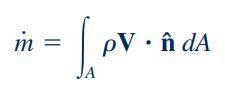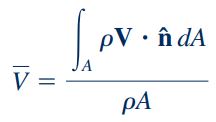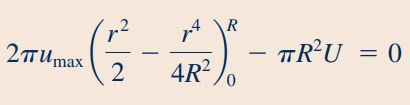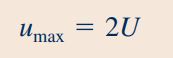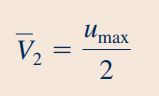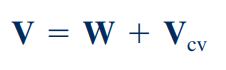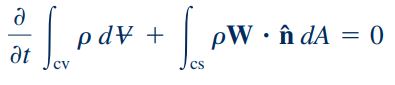پیوستگی و بقای جرم در سیالات

پردیس فناوری کیش_طرح مشاوره متخصصین صنعت و مدیریت_گروه مکانیک

بقای جرم – پیوستگی

در مکانیک سیالات، به یک جز کوچک سیال که شامل تعداد بسیار زیادی مولکول است «حجم کنترل» (Control Volume) می‌گویند. تعریف حجم کنترل و مشخص کردن مرزهای آن، یکی از اساسی‌ترین مسائل در علم مکانیک سیالات برای تعیین معادلات بقای جرم و پیوستگی است و این مطلب به بیان دقیق مفاهیم مرتبط با آن می‌پردازد. در ادامه نشان داده می‌شود که حجم کنترل می‌تواند ساکن و یا متحرک باشد و همچنین شکل آن نیز با زمان تغییر کند.

برای تعریف پیوستگی ابتدا کمیت‌های شدتی و مقداری را تعریف می‌کنیم. «کمیت شدتی» (Intensive Property)، خاصیتی از یک ماده است که به اندازه سیستم و یا مقدار آن ماده بستگی نداشته باشد. برای مثال، دما و چگالی یک جسم با نصف کردن آن جسم تغییر نمی‌کنند، بنابراین این دو خاصیت، کمیت‌های شدتی هستند. به خواصی که اندازه آن‌ها به اندازه سیستم و یا مقدار ماده بستگی دارند «کمیت‌های مقداری» (Extensive Property) می‌گویند. برای مثال، جرم، حجم و گرمای منتقل شده از جسم کمیت‌های مقداری هستند.

معادله پیوستگی به صورت کلی، تغییرات یک کمیت شدتی مانند L را در یک سیستم بیان می‌کند. لازم به ذکر است که سیستم به صورت مجموعه‌ای از اجزا تعریف می‌شود که ویژگی‌های اساسی این اجزا در طول زمان بدون تغییر باقی می‌مانند. برای بیان معادله پیوستگی ابتدا به بررسی مفهوم «بقای جرم» (Conservation of Math) می‌پردازیم. معادله بقای جرم برای یک سیستم که در یک میدان جریان سیال قرار دارد به شکل زیر قابل تعریف است:

رابطه 1

رابطه ۲

این روابط نشان می‌دهند که جرم سیستم در طول زمان ثابت می‌ماند. همچنین دقت شود که انتگرال نشان داده شده در رابطه بالا، روی حجم سیستم اعمال می‌شود. این معادلات به وضوح بیان می‌کنند که در یک سیستم بسته، جرم سیستم در طول یک فرایند ثابت باقی می‌ماند. در ادامه برای بیان جزئیات روابط بقای جرم و پیوستگی (پایستگی جرم)، از فرم رایج معادله انتقال رینولدز استفاده می‌کنیم. که این معادله به شکل زیر نمایش داده می‌شود:

رابطه ۳

سمت چپ این معادله، نرخ تغییرات کمیت مورد نظر ما در سیستم را بیان می‌کند. ترم اول در سمت راست رابطه بالا، نشان دهنده انتگرال روی حجم کنترل است و شامل ترم‌های «چشمه» (source) و «چاه» (sink) می‌شود. ترم دوم سمت راست معادله انتقال رینولدز نیز نشان دهنده انتگرال‌گیری روی سطح‌های حجم کنترل مورد نظر ما است. این قسمت معادله بیان می‌کند که چه مقدار سیال از مرز‌های حجم کنترل به سمت داخل و یا خارج آن عبور می‌کند.



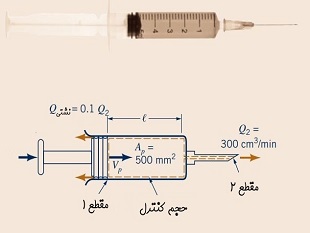
در صورتی که پارامتر مورد نظر در معادله انتقال رینولدز (B) برابر با جرم در نظر گرفته شود، مقدار متغیر  b برابر با یک می‌شود. در نهایت با اعمال معادله انتقال رینولدز روی یک حجم کنترل ثابت و بدون تغییر شکل که در تصویر بالا نشان داده شده است، معادله نهایی به فرم زیر در می‌آید.



سمت چپ معادله بالا، نرخ زمانی تغییرات جرم سیستم را نشان می‌دهد و به صورت مجموع دو ویژگی مهم از حجم کنترل بیان می‌شود که عبارات سمت راست معادله را تشکیل می‌دهند. عبارت اول، نرخ زمانی تغییرات جرم در داخل حجم کنترل را به شکل زیر نشان می‌دهد.



همچنین عبارت دوم، جریان جرمی از طریق مرزهای حجم کنترل را مطابق با معادله زیر نشان می‌دهد.



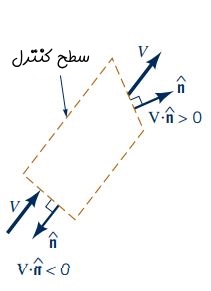
عبارت داخل انتگرال بالا، حاصل ضرب سرعت عمود بر قسمت کوچکی از سطح مقطع ($$V.\hat{n}$$) را در دیفرانسیل سطح مقطع (dA)، نشان می‌دهد. علاوه بر این، همانطور که در شکل زیر نشان داده شده است، در صورتی که مقدار $$V.\hat{n}$$ مثبت باشد، جهت جریان سیال به سمت خارج از مرزهای حجم کنترل است و در صورتی که مقدار $$V.\hat{n}$$ منفی باشد جهت جریان سیال به سمت داخل حجم کنترل است.



بنابراین انتگرال فوق حاصل جمع عبارت $$\rho V.\hat{n}dA$$، روی تمام سطوح حجم کنترل است و می‌توان آن را به فرم زیر نشان داد.



در رابطه بالا، $$\dot{m}$$ جریان جرمی را نشان می‌دهد و می‌توان نتیجه گرفت که اگر عبارت سمت چپ معادله، مقدار مثبتی داشته باشد جریان خالص به سمت خارج از حجم کنترل است و در صورتی که حاصل عبارات سمت چپ معادله، مقداری منفی باشد، جریان خالص به سمت داخل حجم کنترل است.

معادله بقای جرم را می‌توان برای حالت پایا بازنویسی کرد. توجه شود که در حالت پایا، تمامی خواص میدان جریان از جمله چگالی ثابت می‌مانند. بنابراین از ترم اول سمت راست معادله (3) صرف نظر می‌شود. به عبارت دیگر در حالت پایا رابطه زیر برقرار است:



بنابراین برای بیان معادله بقای جرم به فرم حجم کنترلی، معادلات ۱، ۲ و ۳ را با یکدیگر ترکیب می‌کنیم. نتیجه نهایی به فرم رابطه زیر خواهد بود که به آن «معادله پیوستگی» (Continuity Equation) می‌گویند.



محاسبه سرعت متوسط

معمولا برای محاسبه جریان جرمی از یک سطح مقطع مشخص سیال به مساحت A، از رابطه زیر استفاده می‌شود.



در این رابطه $$\rho$$ چگالی، Q دبی حجمی و V سرعت متوسط جریان سیال عمود بر سطح مقطع A است. از رابطه بالا برای محاسبه سرعت (V) و چگالی ($$\rho$$) متوسط یک سیال نیز استفاده می‌شود. در اکثر مسائلی که ما با آن‌ها سر و کار داریم سیال به صورت غیر قابل تراکم در نظر گرفته می‌شود و چگالی آن تغییر نمی‌کند. بنابراین در چنین مسائلی، چگالی نقطه‌ای و متوسط سیال در یک سطح مقطع، یکسان هستند.

برای محاسبه سرعت متوسط سیال عبوری از سطح مقطع A، جریان جرمی محاسبه شده توسط رابطه بالا را با جریان جرمی حاصل از رابطه انتگرالی برابر می‌گذاریم. رابطه انتگرالی محاسبه جریان جرمی که در بخش قبلی به آن اشاره شد، به فرم زیر است.



بنابراین سرعت متوسط سیال مطابق با رابطه زیر محاسبه می‌شود.



مثال

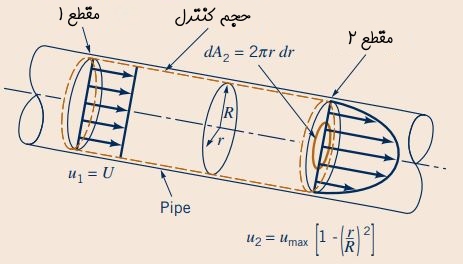
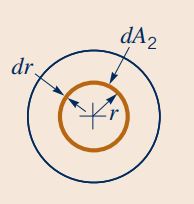
لوله‌ای به شعاع R را مطابق شکل زیر در نظر بگیرید. سیالی غیر قابل تراکم به صورت پایا در آن جریان دارد. در مقطع «1»، سرعت سیال برابر با مقدار ثابت U است و جهت آن در تمامی نقاط، موازی با محور لوله است. در مقطع «2»، پروفیل سرعت سیال به صورت متقارن و سهموی است به طوری که مقدار آن روی دیواره برابر با صفر و در مرکز لوله ماکزیمم ($$u_{max}$$) است. برای راهنمایی، رابطه‌ سرعت بر حسب فاصله از مرکز لوله برای مقطع «2» در شکل نشان داده شده است. در این مسئله ابتدا رابطه بین سرعت مقطع «۱» (U) و ماکزیمم سرعت مقطع «2» ($$u_{max}$$) را بیابید. سپس به محاسبه رابطه بین سرعت متوسط در مقطع «2» و و $$u_{max}$$ بپردازید.



انتخاب مناسب حجم کنترل، اولین گام برای پاسخ به این مسئله است. حجم کنترل مورد نظر در شکل بالا با خط‌چین نمایش داده شده است. در ابتدا رابطه پیوستگی که در بخش قبلی بیان کردیم را برای این حجم کنترل می‌نویسیم. توجه به این نکته ضروری است که ترم اول معادله پیوستگی برای جریان پایا برابر با صفر است. بنابراین داریم:

1

در مقطع «1» سرعت سیال، مقداری ثابت و برابر با U دارد، بنابراین معادله پیوستگی در مقطع «1» به صورت رابطه زیر بیان می‌شود:

2

سرعت سیال در مقطع «۲» یکنواخت نیست و برای محاسبه انتگرال موجود در معادله پیوستگی، نیاز به تعیین dA است. بنابراین dA را مطابق با شکل زیر به صورت یک واشر به شعاع r و ضخامت dr در نظر می‌گیریم. این واشر مساحتی برابر با dA دارد.



بنابراین دبی جرمی عبوری از مقطع ۲ با استفاده از رابطه زیر قابل محاسبه است.

3

دبی جرمی عبوری از مقطع‌های ۱ و ۲ باهم برابر هستند. بنابراین با ترکیب معادلات ۱، ۲ و ۳ رابطه زیر برای سیال به دست می‌آید.

4

در ادامه با توجه به فرض غیر قابل تراکم بودن سیال، چگالی مقطع‌های «1» و «2» را با یکدیگر برابر قرار می‌دهیم و در نهایت رابطه سرعت مقطع «2» که به صورت سهومی است را در رابطه بالا وارد می‌کنیم.

5

با انتگرال گیری از رابطه بالا در طول شعاع لوله به رابطه زیر می‌رسیم و ارتباط بین سرعت مقطع «۱» (U) و ماکزیمم سرعت مقطع «2» ($$u_{max}$$) به دست می‌آید.



روش عمومی محاسبه سرعت متوسط در سیالات، استفاده از رابطه‌ای است که در درس‌نامه ارائه شد. در اینجا می‌دانیم که سیال مورد نظر در این مسئله غیر قابل تراکم است و در این شرایط، سرعت متوسط سیال در تمامی مقاطع لوله یکسان در نظر گرفته می‌شود. بنابراین رابطه بین سرعت متوسط در مقطع «2» و و $$u_{max}$$ به فرم زیر قابل محاسبه است.



تعمیم معادله پیوستگی برای حجم کنترل متحرک و بدون تغییر شکل

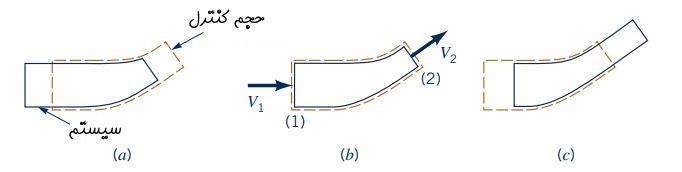
در قسمت‌های قبل، معادله پیوستگی را در حالتی بیان کردیم که حجم کنترل ثابت بود و تغییر شکلی در آن رخ نمی‌داد. در ادامه به بررسی معادله پیوستگی با فرض حجم کنترل متحرک و بدون تغییر شکل می‌پردازیم و روابط حاکم بر آن را مورد بررسی قرار می‌دهیم. همانطور که در قسمت قبلی اشاره شد انتخاب حجم کنترل مناسب، مهمترین گام در پاسخگویی به مسائل مکانیک سیالات است و در صورتی که حجم کنترل به درستی انتخاب نشده باشد، محاسبات لازم چندین برابر خواهند شد. این موضوع در قالب مثال‌، مورد بررسی قرار گرفته است.

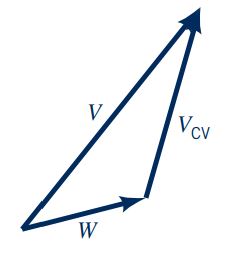
در برخی از مسائل انتخاب حجم کنترل متصل به مرجع متحرک، موجب سادگی راه حل مسئله می‌شود. برای مثال یک هواپیمای در حال حرکت را در نظر بگیرید. در صورتی که حجم کنترل، موتور جتی باشد که با هواپیما در حال حرکت است، مسئله به سادگی قابل حل است. مهم‌ترین پارامتر در این مسائل، سرعت سیال نسبت به حجم کنترل متحرک است که برای محاسبه آن می‌توان از رابطه زیر استفاده کرد. در این رابطه، ارتباط بین سرعت‌های مختلف نشان داده شده است.



W سرعت نسبی سیال را نشان می‌دهد و برابر با سرعتی است که توسط ناظر متحرک با حجم کنترل، دیده می‌شود. $$V_{cv}$$ سرعت حجم کنترل را نشان می‌دهد که برابر با سرعت حجم کنترل نسبت به ناظر ساکن است. V نیز سرعت مطلق سیال است که نسبت به ناظر ساکن اندازه‌گیری می‌شود.

برای محاسبه معادله پیوستگی، رابطه بین سرعت‌ها که در معادله بالا نشان داده شده است را در معادله انتقال رینولدز وارد می‌کنیم. در نهایت رابطه پیوستگی اصلاح شده، به فرم زیر در می‌آید: