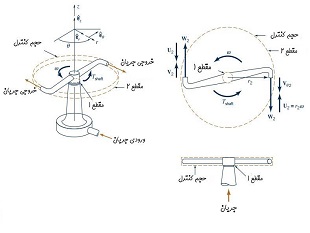
مومنتوم زاویه ای
پردیس فناوری کیش_طرح مشاوره متخصصین صنعت و مدیریت_گروه مکانیک
معادله مومنتوم زاویهای
در بسیاری از مسائل مهندسی، «گشتاور» (Torque) حول یک محور، مفهوم بسیار مهمی است که با استفاده از رابطه <span id="MathJax-Element-1-Frame" class="mjx-chtml MathJax_CHTML" style="font-family: IRANSans !important;font-size: 17px !important;line-height: 0;text-indent: 0px;text-align: center;text-transform: none;font-style: normal;font-weight: normal;letter-spacing: normal;float: none;direction: ltr;max-width: none;max-height: none;min-width: 0px;min-height: 0px;border: 0px;margin: 0px;padding: 1px 0px" role="presentation" data-mathml="T=r→×F→">T=r→×F→ محاسبه میشود. در این رابطه <span id="MathJax-Element-2-Frame" class="mjx-chtml MathJax_CHTML" style="font-family: IRANSans !important;font-size: 17px !important;line-height: 0;text-indent: 0px;text-align: center;text-transform: none;font-style: normal;font-weight: normal;letter-spacing: normal;float: none;direction: ltr;max-width: none;max-height: none;min-width: 0px;min-height: 0px;border: 0px;margin: 0px;padding: 1px 0px" role="presentation" data-mathml="r→">r→ بردار فاصله نیرو تا محور و <span id="MathJax-Element-3-Frame" class="mjx-chtml MathJax_CHTML" style="font-family: IRANSans !important;font-size: 17px !important;line-height: 0;text-indent: 0px;text-align: center;text-transform: none;font-style: normal;font-weight: normal;letter-spacing: normal;float: none;direction: ltr;max-width: none;max-height: none;min-width: 0px;min-height: 0px;border: 0px;margin: 0px;padding: 1px 0px" role="presentation" data-mathml="F→">F→ بردار نیرو را نشان میدهند. در مطلب «مومنتوم خطی در سیالات» برای محاسبه معادله مومنتوم خطی از قانون دوم نیوتن استفاده کردیم و به روابط قابل استفاده برای مسائل مکانیک سیالات دست یافتیم.
در این مطلب، هدف تعیین معادله مومنتوم زاویهای است. این معادله را میتوان با ضرب طرفین معادله مومنتوم خطی در فاصله نیرو از محور دوران محاسبه کرد. بنابراین برای شروع، قانون دوم نیوتن برای یک ذره سیال را به فرم زیر مینویسم:
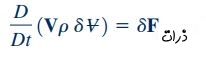
در این رابطه، V سرعت ذره سیال است که در یک سیستم مختصات لَخت محاسبه میشود. عبارت سمت راست رابطه بالا، نیروی خارجی که بر این ذره وارد میشود را نشان میدهد. در ادامه و برای محاسبه مومنتوم زاویهای، گشتاور دو سمت رابطه فوق را نسبت به محور با فاصله r از آن، محاسبه میکنیم. برای این منظور، معادله بالا را به صورت ضرب خارجی r در دو طرف رابطه و به شکل زیر بازنویسی میکنیم.
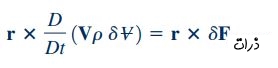
رای سادهسازی رابطه بالا نیاز به استفاده از روابط ریاضی و مفهوم ضرب خارجی داریم. یکی از ویژگیهای ضرب خارجی در ریاضیات، در رابطه زیر نشان داده شده است.
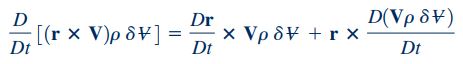
برای سادهسازی رابطه بالا از این نکته استفاده میکنیم که حاصل مشتق مادی r برابر با V میشود. بنابراین عبارت اول سمت راست رابطه فوق به صورت حاصل ضرب خارجی عبارت V در خودش در میآید که میتوان آن را به فرم زیر نمایش داد.
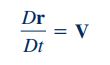
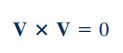
بنابراین در صورتی که روابط 3، 4 و 5 در رابطه 2 قرار داده شوند، معادله مومنتوم زاویهای به فرم زیر بازنویسی میشود.
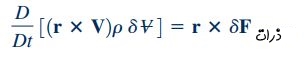
رابطه فوق برای تمام ذراتی که در یک سیستم حضور دارند، صادق است. بنابراین این رابطه را میتوان برای کل سیستم بازنویسی کرد. برای این منظور باید مومنتوم زاویهای سیستم، به صورت مجموع مومنتوم زاویهای تک تک ذرات تشکیل دهنده آن سیستم نوشته شود که این کار با استفاده از رابطه انتگرالی زیر انجام میشود.
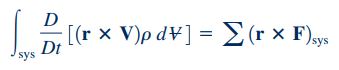
در مکانیک سیالات با توجه به تعاریف سیستم و مشتق مادی، روابط زیر برای ذرات یک سیستم و مشتق مادی آن سیستم برقرار هستند.
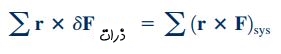
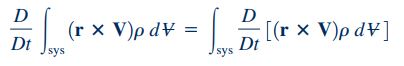
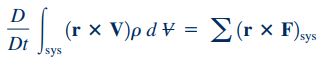
سمت چپ این معادله، نرخ زمانی تغییرات مومنتوم زاویهای سیستم را نمایش میدهد و عبارت سمت راست این معادله نشاندهنده مجموع گشتاور نیروهای خارجی است که به سیستم وارد میشود. نکته مهم دیگر این است که، گشتاور وارد بر یک حجم کنترل که به سیستم چسبیده است با گشتاور وارد بر آن سیستم برابر است.
کاربرد معادله مومنتوم زاویهای در حل مسائل
معادله مومنتوم زاویهای که در این بخش به بررسی آن پرداخته شد، در حل مسائل مربوط به ماشینهای چرخان مانند توربوماشینها، پرههای توربین و کمپرسور و آبپاشهای چمن به صورت رایج مورد استفاده قرار میگیرد. در هرکدام از مسائل با توجه به شرایط خاص آن مسئله، معادله مومنتوم زاویهای به شکلهای مختلف اصلاح میشود.
در برخی از مسائل برای سادهسازی حل، جریان به صورت یک بعدی در نظر گرفته میشود. در این حالت توزیع یکنواختی از سرعت متوسط در هر بخش جریان موجود است و ضرب خارجی موجود در رابطه مومنتوم زاویهای به صورت ساده قابل محاسبه است.
در گروهی دیگر از مسائل مکانیک سیالات برای سادهسازی معادله مومنتوم زاویهای، جریان به صورت پایا در نظر گرفته میشود. در این حالت عبارت اول سمت چپ معادله مومنتوم زاویهای به شکل زیر نوشته میشود و برابر با صفر است.