تغییر شکل در مهندسی مکانیک

پردیس فناوری کیش_طرح کشاوره متخصصین صنعت و مدیریت_گروه مکانیک

یکی از مفاهیم مهم در زمینه تغییر شکل مواد، «کرنش» است. کرنش، تغییر شکل یک جسم را با توجه به جابجایی نسبی ذرات نمایش می‌دهد و حرکات جسم صلب را در نظر نمی‌گیرد. معادله‌های مختلفی برای تعریف «میدان کرنش» ارائه شده است که انتخاب هر یک، به نحوه تعریف کرنش (با توجه به پیکربندی اولیه یا نهایی) و در نظر گرفتن «تانسور متریک» () یا «دوگان تانسور»  بستگی دارد.

میدان تغییر شکل در جسم پیوسته، بر اثر وجود میدان تنش (ناشی از نیروهای اعمالی) یا تغییرات میدان دمای درون آن جسم ایجاد می‌شود. رابطه بین تنش و کرنش القایی، با استفاده از معادلات مشخصه‌ای مانند قانون هوک برای مواد الاستیک خطی بیان می‌شود. به تغییر شکلی که بعد از حذف میدان تنش بازیابی شود، تغییر شکل الاستیک گفته می‌شود. جسم پیوسته در این حالت، به طور کامل به حالت پیکربندی اولیه خود بازمی‌گردد.

ر طرف مقابل، تغییر شکل‌هایی وجود دارند که حتی پس از حذف تنش‌های اعمالی نیز قابل بازیابی نخواهند بود. یکی از انواع تغییر شکل‌های غیر قابل بازگشت، تغییر شکل پلاستیک است. تغییر شکل پلاستیک زمانی رخ می‌دهد که بیش از حد الاستیک یا تنش تسلیم به جسم نیرو وارد شده باشد. این وضعیت، موجب «لغزش» یا «نابجایی»  اتم‌های درون جسم خواهد شد. یکی دیگر از انواع تغییر شکل‌های غیر قابل برگشت، «تغییر شکل ویسکوز»  است که بخش برگشت‌ناپذیر در تغییر شکل «ویسکوالاستیک» محسوب می‌شود. در تغییر شکل‌های الاستیک، تابع پاسخی که کرنش را به تنش متصل می‌کند، همان «تانسور انطباق»  ماده نام دارد.

کرنش

کرنش، مقدار تغییر شکلی است که جابجایی بین ذرات درون یک جسم را نسبت به یک طول مرجع (طول اولیه یا طول در یک زمان مشخص) بیان می‌کند. تغییر شکل عمومی یک جسم را می‌توان به صورت معادله زیر نوشت:

پارامتر X، موقعیت مرجع نقاط درون جسم است. در این معادله، مرز مشخصی بین حرکات جسم صلب (انتقال و دوران) و تغییرات شکل و اندازه جسم وجود ندارد. به خاطر داشته باشید که تغییر شکل دارای واحد طول است.

معادله کرنش را می‌توان به صورت زیر بیان کرد:

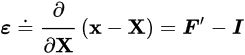
در معادله بالا، I، تانسور همانی است. از این‌رو، کرنش پارامتری بدون بعد به حساب می‌آید و معمولاً به صورت کسر اعشاری، درصد یا بخش در واحد اندازه‌گیری (مانند یک در هزار) بیان می‌شود. کرنش، میزان اختلاف یک تغییر شکل معین در یک محل خاص را نسبت به تغییر شکل جسم صلب نشان می‌دهد.

کرنش به طور کلی یک کمیت تانسور محسوب می‌شود. برای داشتن یک تصویر ذهنی مناسب از کرنش، می‌توان آن را به دو مؤلفه نرمال و برشی تجزیه کرد. در یک جسم تغییر شکل یافته، میزان کشش یا فشار وارده در راستای المان‌های خطی یا الیاف یک جسم، کرنش نرمال است. از سوی دیگر، میزان انحراف ناشی از لغزش لایه‌های مختلف جسم بر روی یکدیگر، به عنوان کرنش برشی شناخته می‌شود. اگر ماده‌ای در حین بارگذاری افزایش طول پیدا کند، از عبارت کرنش کششی برای بیان نوع کرنش نرمال استفاده می‌شود. در طرف مقابل و در صورت وجود تراکم یا کاهش طول در ماده، عبارت کرنش فشاری برای بیان نوع کرنش نرمال به کار برده می‌شود.

تعاریف کرنش

بر اساس میزان کرنش یا تغییر شکل موضعی در یک جسم، تجزیه و تحلیل تغییر شکل را می‌توان به سه نظریه زیر تقسیم‌بندی کرد:

1.نظریه کرنش بی نهایت کوچک:این نظریه با عناوینی همچون «نظریه کرنش کوچک» «نظریه تغییر شکل کوچک» و «نظریه جابجایی کوچک» نیز شناخته می‌شود که در آن، کرنش و چرخش درون جسم مقدار کوچکی است. در این شرایط می‌توان پیکربندی‌های تغییر شکل یافته و بدون تغییر را یکسان در نظر گرفت. برای تجزیه و تحلیل تغییر شکل موادی با رفتار الاستیک از جمله فولاد و بتن که در مهندسی مکانیک و عمران به کار می‌روند، نظریه کرنش بی‌نهایت کوچک مورد استفاده قرار می‌گیرد.

2.نظریه تنش محدود:این نظریه با عناوینی همچون «نظریه کرنش بزرگ»و «نظریه تغییر شکل بزرگ» نیز شناخته می‌شود و با تغییر شکل‌هایی سر و کار دارد که کرنش و چرخش در جسم مقدار بزرگی باشد. در این وضعیت، تفاوت قابل توجهی بین پیکربندی‌های تغییر شکل یافته و بدون تغییر در جسم پیوسته وجود خواهد داشت و مرز بین این دو حالت کاملاً قابل تشخیص خواهد بود. این نظریه بیشتر برای مواد الاستومتر، موادی با تغییر شکل پلاستیک، سیالات و بافت‌های نرم بیولوژیکی کاربرد دارد.

3.نظریه جابجایی بزرگ:این نظریه با عناوینی همچون «نظریه کرنش بزرگ»  و «نظریه تغییر شکل بزرگ» نیز شناخته می‌شود و با تغییر شکل‌هایی سر و کار دارد که کرنش و چرخش در جسم مقدار بزرگی باشد. در این وضعیت، تفاوت قابل توجهی بین پیکربندی‌های تغییر شکل یافته و بدون تغییر در جسم پیوسته وجود خواهد داشت و مرز بین این دو حالت کاملاً قابل تشخیص خواهد بود. این نظریه بیشتر برای مواد الاستومتر، موادی با تغییر شکل پلاستیک، سیالات و بافت‌های نرم بیولوژیکی کاربرد دارد.

در هر یک از نظریه‌های بالا، کرنش به صورت متفاوتی تعریف می‌شود. مفهوم «کرنش مهندسی»، رایج‌ترین مفهومی است که در حوزه مهندسی مکانیک و سازه مورد استفاده قرار می‌گیرد. در حوزه‌های اشاره شده، مقدار تغییر شکل‌های مورد بررسی بسیار کوچک است. از سوی دیگر، برای موادی از قبیل الاستومرها و پلیمرها که در معرض تغییر شکل‌های بزرگ قرار دارند، مفهوم کرنش مهندسی (کرنش‌های مهندسی بالاتر از 1 درصد) قابل استفاده نیست. در این موارد، از مفاهیم پیچیده‌تری مانند «کشش» ، کرنش لگاریتمی، «کرنش گرین و «کرنش آلمانسی» استفاده می‌شود.

کرنش مهندسی

کرنش کوشی یا کرنش مهندسی به صورت نسبت تغییر شکل کل جسم تحت بارگذاری به ابعاد اولیه آن تعریف می‌شود. برای المان‌های خطی مواد یا الیافی که به طور محوری تحت بارگذاری قرار گرفته‌اند، کرنش نرمال مهندسی (e) به صورت تغییرات طول (ΔL) نسبت به طول اولیه (L) آن المان‌های خطی یا الیاف تعریف می‌شود. این کرنش را با عناوین دیگری از جمله «کرنش کششی مهندسی» و «کرنش اسمی» نیز معرفی می‌کنند. در صورتی که الیاف ماده کشیده شوند، علامت کرنش نرمال مثبت و در صورت فشرده شدن این الیاف، علامت کرنش نرمال منفی خواهد بود. به این ترتیب، کرنش نرمال را می‌توان با استفاده از رابطه زیر محاسبه کرد:

e: کرنش نرمال مهندسی؛ L: طول اولیه الیاف جسم؛ l: طول نهایی الیاف

نسبت کشش

نسبت کشش، معیاری برای اندازه‌گیری کرنش کششی یا نرمال یک المان خطی است که می‌تواند برای هر دو پیکربندی تغییر شکل یافته و بدون تغییر تعریف شود. این پارامتر، نسبت طول نهایی (l) به طول اولیه ماده (L) است.

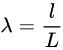
رابطه نسبت کشش با کرنش مهندسی به صورت زیر است:

رابطه نسبت کشش با کرنش مهندسی به صورت زیر است:

نسبت کشش برای تجزیه و تحلیل موادی مانند الاستومترها به کار می‌رود که تغییر شکل‌های بزرگی را از خود به نمایش می‌گذارند و می‌توانند نسبتی بین 3 یا 4 را پیش از رسیدن به نقطه شکست خود تحمل کنند. در طرف مقابل، شکست مواد رایج در مهندسی مکانیک و سازه (فولاد و بتن)، در نسبت‌های بسیار پایین‌تری رخ می‌دهد.

کرنش واقعی

کرنش لگاریتمی (ε)، با عناوین دیگری مانند کرنش واقعی یا «کرنش هِنکی»  نیز شناخته می‌شود. یک کرنش تفاضلی مانند معادله زیر را در نظر بگیرید:

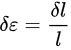
کرنش لگاریتمی را می‌توان با انتگرال‌گیری از این کرنش افزایشی (مانند معادله زیر) محاسبه کرد:

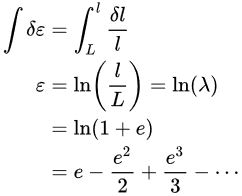
در معادله بالا، e، کرنش مهندسی است. هنگامی که یک سری کرنش تدریجی بر روی یک جسم اعمال می‌شود، کرنش لگاریتمی می‌تواند با در نظر گرفتن تأثیر مسیر کرنش، مقدار دقیق کرنش نهایی را محاسبه کند.

مفهوم تغییر شکل

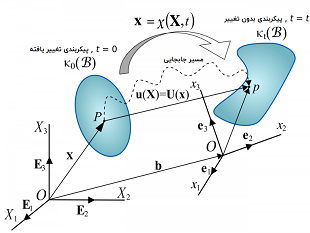
تغییر شکل، تغییر در ابعاد یک جسم پیوسته است. فرض کنید که محل اولیه و نهایی قرارگیری یک جسم را با استفاده از خطوطی مشخص کنیم. در این وضعیت، تغییر شکل می‌تواند باعث تغییر در اندازه این خطوط شود. به حالتی که هیچ تغییری در طول خطوط مشاهده نشود، جابجایی جسم صلب گفته می‌شود.

در تحلیل تغییر شکل‌ها، استفاده از یک پیکربندی مرجع یا وضعیت هندسی اولیه، بررسی پیکربندی و تغییرات بعدی را راحت‌تر می‌کند. معمولاً پیکربندی جسم در t=0 را به عنوان پیکربندی مرجع، κ0(B)، در نظر می‌گیرند.

برای تجزیه و تحلیل تغییر شکل، پیکربندی مرجع، با عنوان پیکربندی بدون تغییر و پیکربندی فعلی، با عنوان پیکربندی تغییریافته شناخته می‌شود. علاوه بر این، در هنگام تحلیل تغییر شکل، پارامتر زمان در نظر گرفته نمی‌شود. از این‌رو، پیکربندی‌های موجود در بین حالت تغییر یافته و بدون تغییر، مد نظر قرار نمی‌گیرند.

به مؤلفه‌های Xi در بردار مکان X برای یک ذره با پیکربندی و سیستم مختصات مرجع، مختصات مادی یا مختصات مرجع گفته می‌شود. در طرف مقابل، مؤلفه‌های xi در بردار مکان x برای یک ذره با پیکربندی تغییر یافته و سیستم مختصات فضایی مرجع را مختصات فضایی می‌گویند.

دو روش برای تجزیه و تحلیل تغییر شکل در محیط‌های پیوسته وجود دارد. یکی از این روش‌ها، بر اساس مختصات مادی یا مرجع تعریف شده است که به آن «توصیف مادی»  یا «توصیف لاگرانژی» گفته می‌شود. روش دوم، بر اساس مختصات فضایی المان مورد تحلیل تعریف شده است که به آن «توصیف فضایی»  یا «توصیف اویلری» می‌گویند.

در حین تغییر شکل یک محیط پیوسته، جسم مورد نظر همیشه دارای پیوستگی است. دلایل این امر را می‌توان به صورت زیر بیان کرد:

1. نقاطی از ماده که در هر لحظه از زمان تشکیل یک منحنی بسته را می‌دهند، در زمان‌های بعدی نیز همیشه یک منحنی بسته را تشکیل خواهند داد.

2. نقاطی از ماده که در هر لحظه از زمان تشکیل یک سطح بسته را می‌دهند، در زمان‌های بعدی نیز همیشه یک سطح بسته را تشکیل خواهند داد. به علاوه، مواد موجود در این سطح، همیشه درون محدوده آن باقی خواهند ماند.

جابجایی

در یک جسم پیوسته، جابجایی منجر به تغییر پیکربندی خواهد شد. جابجایی یک جسم، دارای دو مؤلفه جابجایی جسم صلب و تغییر شکل است. در جابجایی جسم صلب، انتقال و چرخش جسم به صورت هم‌زمان و بدون تغییر در شکل و اندازه آن رخ می‌دهد. تغییر شکل یک جسم، تغییر در شکل و یا اندازه آن از پیکربندی اولیه یا بدون تغییر κ0(B) به پیکربندی فعلی یا تغییر یافته κt(B) را نشان می‌دهد (شکل زیر).

در صورتی که پس از جابجایی یک محیط پیوسته، بین ذرات یک جابجایی نسبی مشاهده شود، تغییر شکل رخ داده است. از طرف دیگر، اگر پس از جابجایی یک محیط پیوسته، جابجایی نسبی بین ذرات صفر باشد، هیچ تغییر شکلی ایجاد نشده و جابجایی جسم صلب رخ داده است. به برداری که موقعیت‌های مکانی یک ذره (P) در پیکربندی بدون تغییر و پیکربندی تغییر یافته را به هم متصل می‌کند، بردار جابجایی u(X,t) = uiei در توصیف لاگرانژی یا U(x,t) = UJEJ در توصیف اویلری گفته می‌شود.

میدان جابجایی، میدان برداری تمام بردارهای جابجایی برای ذرات موجود در جسم مورد بررسی است. این میدان، پیکربندی تغییر یافته را به پیکربندی بودن تغییر ارتباط می‌دهد. در تحلیل تغییر شکل یا حرکت یک جسم، استفاده از میدان جابجایی کار را راحت‌تر می‌کند. به طور کلی، رابطه میدان جابجایی را با توجه به مختصات مادی می‌توان به صورت زیر بیان کرد:

خواهیم داشت:

تانسور گرادیان جابجایی

با مشتق‌گیری جزئی بردار جابجایی نسبت به مختصات مادی می‌توان تانسور گرادیان جابجایی ماده (XU∇) را به دست آورد. به این ترتیب، داریم:

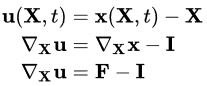
یا

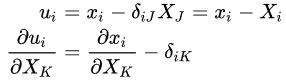
در روابط بالا، F، تانسور گرادیان تغییر شکل است. با مشتق‌گیری جزئی بردار جابجایی نسبت به مختصات فضایی نیز تانسور گرادیان جابجایی فضایی (xU∇) به دست می‌آید. به این ترتیب، داریم:

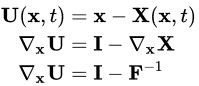
یا

تغییر شکل صفحه‌ای

تغییر شکل صفحه‌ای با عنوان کرنش صفحه‌ای نیز شناخته می‌شود و زمانی رخ می‌دهد که تغییر شکل به یکی از صفحات پیکربندی مرجع محدود شده باشد. در صورتی که تغییر شکل، به صفحه‌ای با بردارهای پایه e1 و e2 محدود شده باشد، گرادیان تغییر شکل به صورت زیر خواهد بود:

فرم ماتریسی معادله بالا به شکل زیر است:

بر اساس نظریه تجزیه قطبی، گرادیان تغییر شکل را می‌توان به یک کشش و یک چرخش تجزیه کرد. از آنجایی که تمام تغییر شکل‌ها درون یک صفحه رخ می‌دهند، می‌توان نوشت:

Θ: زاویه دوران؛ λ1 و λ2: کشش‌های اصلی

تغییر شکل صفحه‌ای با حجم ثابت

اگر تغییر شکل با حجم ثابت باشد، det(F)=1 خواهد بود. به این ترتیب، خواهیم داشت:

این رابطه را می‌توان به صورت زیر نیز نوشت:

برش ساده

یک تغییر شکل صفحه‌ای با حجم ثابت را در نظر بگیرید. اگر هیچ تغییری در طول و جهت‌گیری مجموعه‌ای از المان‌های خطی با یک جهت‌گیری مرجع مشخص رخ ندهد، تغییر شکل برش ساده اتفاق افتاده است. در صورتی که e1، جهت مرجع ثابت در المان‌های خطی بدون تغییر باشد، λ1 = 1 و F.e1 = e1 خواهد بود. بنابراین:

از آنجایی که تغییر شکل با حجم ثابت است، داریم:

و

به این ترتیب، گرادیان تغییر شکل در برش ساده را می‌توان به صورت زیر تعریف کرد:

در این صورت، داریم:

از آنجایی که رابطه زیر برقرار است:

می‌توانیم گرادیان تغییر شکل را به صورت زیر بازنویسی کنیم: